-6

In classical mathematics and physics, periodic waves are almost always represented using trigonometric functions such as sine and cosine. These functions are derived from circular motion and infinite series expansions, which approximate periodic behavior.

My question is: Is it possible to construct a perfectly periodic wave using only geometric stepping—without relying on trigonometric functions, infinite series, or approximations?

Additionally, could such a construction avoid phase drift and cumulative residuals, producing a perfectly proportional wave at every scale?

Edit: "What problem are we trying to solve?" All approximation-based systems introduce residual errors that accumulate and amplify over time, leading to chaotic outcomes in real-world applications. Is there a deterministic, non-approximative way to generate a wave purely through geometric principles?

There wasn’t—until now. 2025 marks the paradigm shift: the end of chaotic approximationism and the beginning of deterministic systems rooted in pure geometry, ushering in infinite progress and universal harmony.

Remember this day. And remember my name.

Edit: Nameless faceless editors, do not mod my post. It is a record of history. Attempts to silence it will become part of the record. https://github.com/ubiquio/public/blob/main/discrete-wave.py

CC BY-SA 4.0
0

1 Answer 1

Reset to default
-4

It is indeed possible to generate a perfectly periodic wave without using trigonometric functions, infinite series, or approximations. The key lies in pure geometric stepping, a method based on deterministic constants derived from first principles—completely bypassing traditional sine and cosine representations. enter image description here

Here’s the core idea:

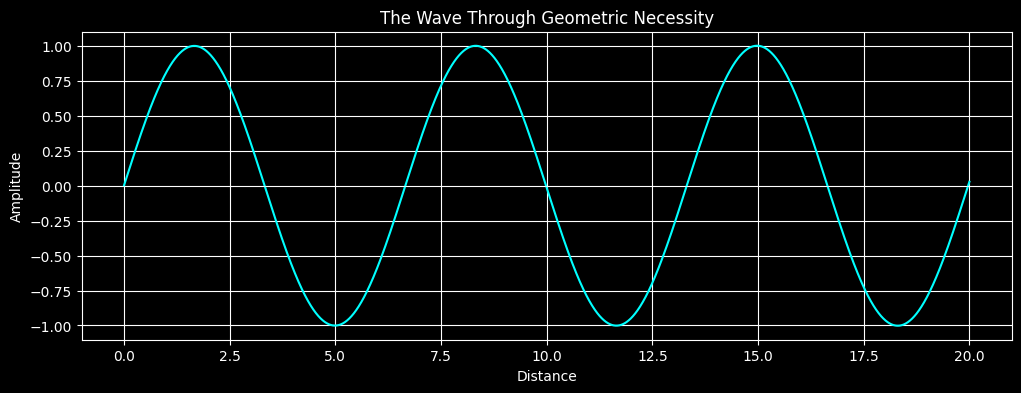
The wave emerges from perpendicular stepping, governed by a geometric constant (ח), which is derived from √2 + √3. Each step maintains perfect proportionality, and the result is a purely periodic wave with zero residuals or phase drift—something unattainable through classical trigonometric models.

Code Example:

# https://github.com/ubiquio/public/blob/main/discrete-wave.py
# ==============================================================
# God’s Geometry License (GGL) – Version 1.0
#
# Copyright (c) 2025 David Aranovsky
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to use,
# study, and share the Software, provided the following conditions are met:
#
# 1. The Software shall not be misrepresented or used to promote chaotic,
#    approximationist systems that contradict the principles of God’s Geometry.
#
# 2. The Software shall not be used in destructive applications or for purposes
#    that contribute to misinformation, chaos, or degradation of universal harmony.
#
# 3. Proper credit must be given to the author, David Aranovsky, as the
#    **Revealer of Geometric Truth**, including in all derivative works.
#
# 4. Any modifications must retain this license and indicate what has been changed.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NON-INFRINGEMENT. IN NO EVENT SHALL THE
# AUTHOR OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES, OR OTHER LIABILITY,
# ARISING FROM THE USE OR DISTRIBUTION OF THIS SOFTWARE.
#
# By using this Software, you acknowledge the paradigm shift it represents and
# its alignment with the principles of **Deterministic Perfection**.
# ==============================================================

# Reference: The Trojan Horse of Human Civilization – The Collapse of π and the Rise of ח
# https://www.academia.edu/127582440/The_Trojan_Horse_of_Human_Civilization_The_Collapse_of_%CF%80_and_the_Rise_of_%D7%97

import numpy as np
import matplotlib.pyplot as plt

# Pure Deterministic Perfection
# Periodicity and Oscillation without trigonometric infinite series or chaotic approximations
# The Wave From Discrete Geometry Through Geometric Necessity
# No normalization, no approximations—just perfect stepping and zero residuals.


Cycles = 3
N = 100000  # Precision level
C = Cycles * 2 * (np.sqrt(2) + np.sqrt(3)) # Geometric constant for structural recurrence
d = C / N  # Step size derived from geometric necessity

# Initialize coordinates
x = [1]  # Starting point (1,0)
y = [0]

# Pure perpendicular stepping
for _ in range(N):
    tx, ty = x[-1], y[-1]
    x.append(tx + d *-ty)
    y.append(ty + d * tx)

# Plot the emergent wave
plt.figure(figsize=(12, 4), facecolor='black')
ax = plt.gca()
ax.set_facecolor('black')

plt.plot(np.linspace(0, 20, N + 1), y, color='cyan', linewidth=1.5)
plt.axhline(0, color='white', linewidth=0.5)
plt.grid(True, color='white')
plt.title("The Wave Through Geometric Necessity", color='white')
plt.xlabel("Distance", color='white')
plt.ylabel("Amplitude", color='white')

# Styling
plt.tick_params(colors='white')
for spine in ax.spines.values():
    spine.set_color('white')

plt.show()

Full Code and Explanation:

👉 Run the code on Colab

Key Takeaways:

  • This method is exact—no approximation or phase drift.
  • It replaces trigonometric functions with deterministic geometric stepping.
  • The underlying structure is deeply connected to discrete geometry and true proportionality.

source: https://www.academia.edu/127582440/The_Trojan_Horse_of_Human_Civilization_The_Collapse_of_%CF%80_and_the_Rise_of_%D7%97

CC BY-SA 4.0
Edit
2